Class 12 Physics: Electric Charge & Electronics

 Electric Charge and Material Science   Fundamentals 

“From Subatomic Particles to Semiconductors”

---

🌟 1. What Is Electric Charge?

Electric charge is one of the most fundamental properties of matter. It is responsible for creating electric and magnetic fields, which in turn produce electromagnetic force—one of the four fundamental forces of nature (along with gravity, strong nuclear, and weak nuclear forces).

Every object in the universe is made up of atoms, and these atoms consist of subatomic particles:

• Protons (positively charged)

• Electrons (negatively charged)

• Neutrons (no charge)

The net electric charge of an object determines how it interacts with other charged particles. If an object has more electrons than protons, it is negatively charged. If it has more protons, it is positively charged. If both are equal, it is neutral.

---

🔹 2. Types of Electric Charge

There are two types of electric charge:

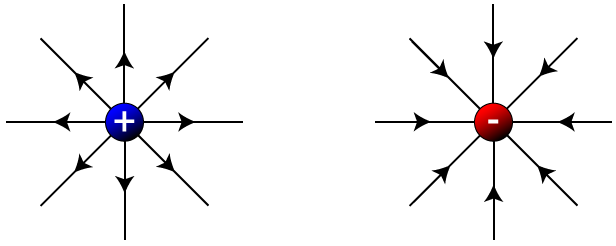
🧲 Positive Charge:

• Carried by protons.

• Found in the nucleus of atoms.

• Cannot move freely in solids (they are bound inside the nucleus).

🧲 Negative Charge:

• Carried by electrons.

• Found outside the nucleus in electron clouds.

• These are mobile and are responsible for electrical conduction in metals and semiconductors.

⚖️ Neutral Charge:

• When the number of protons equals the number of electrons.

• No net electric force is exerted.

These charges interact via electrostatic forces—positive and negative charges attract, while like charges repel.

---

🔹 3. SI Unit of Electric Charge

The SI (International System) unit of electric charge is the Coulomb (C).

⚡ 1 Coulomb =

The amount of charge transferred by a current of 1 ampere flowing for 1 second.

$$1 \, \text{C} = 1 \, \text{A} \cdot 1 \, \text{s}$$

In practical terms, 1 C is a very large amount of charge. The charge on one electron is:

$$e = 1.602 \times 10^{-19} \, \text{C}$$

So, $1 \, \text{C}$ equals approximately 6.24 × 10¹⁸ electrons!

---

🔹 4. Elementary Charge

The elementary charge, denoted as $e$, is the smallest unit of electric charge that exists freely.

• Charge of a proton:

  $$+e = +1.602 \times 10^{-19} \, \text{C}$$

• Charge of an electron:

  $$-e = -1.602 \times 10^{-19} \, \text{C}$$

All charges in nature are integer multiples of this elementary charge. This is called the quantization of charge.

---

🔹 5. Properties of Electric Charge

Electric charge is a fundamental property of matter that plays a central role in electromagnetic interactions. It cannot be seen directly, but its effects are observed through the forces and fields it creates.

Here are the  key properties of electric charge:

---

✅ (i) Electric Charge – Intrinsic Property

• Electric charge is an intrinsic and fundamental property of subatomic particles like electrons and protons.

• Electrons carry negative charge (−e) and protons carry positive charge (+e).

• SI unit of charge is the coulomb (C).

  $$1 \, \text{C} = 6.24 \times 10^{18} \, \text{electrons}$$

This property is unchanging for each type of particle—electrons always carry the same charge, no matter where they are.

---

♻️ (ii) Conservation of Charge

• Charge can neither be created nor destroyed, only transferred from one object to another.

• For example:

  • When a glass rod is rubbed with a silk cloth, electrons are transferred from the glass to the silk.

  • As a result, the glass becomes positively charged (losing electrons) and the silk becomes negatively charged (gaining electrons).

🧠 Important:
The total charge before and after remains the same. This means:

$$\text{Total charge before} = \text{Total charge after}$$

This is known as the Law of Conservation of Electric Charge.

---

📏 (iii) Quantisation of Charge

• Electric charge always exists in discrete packets.

• The smallest unit of charge is the elementary charge:

  $$e = 1.6 \times 10^{-19} \, \text{C}$$

• Any charge $q$ must be an integer multiple of e:

  $$q = n \cdot e \quad \text{where } n = 0, \pm1, \pm2, \pm3, \dots$$

This is called the quantisation of charge—you will never find a charge like 0.5e or √2e on an isolated particle.

---

           Basic Properties of  Electric Charge Summary 

⚙️ 1. Quantization of Charge

Electric charge only exists in discrete packets—integral multiples of $e$. No particle can have a charge like 0.5e.

$$q = n \cdot e \quad (n = 0, \pm1, \pm2, \ldots)$$

⚙️ 2. Conservation of Charge

In a closed system, the total electric charge remains constant, no matter what processes occur. Charge can be transferred, but not created or destroyed.

⚙️ 3. Additivity of Charge

If a body has multiple point charges, the total charge is the algebraic sum of all charges.

$$Q_{\text{total}} = q_1 + q_2 + q_3 + \ldots$$

⚙️ 4. Transferability

Charge can move from one object to another through conduction, friction, or induction. This is how static electricity builds up or how current flows in a circuit.

⚙️ 5. Invariance

Charge is a scalar quantity and is independent of the observer's frame of reference—whether the particle is at rest or moving.

---

🔹 6. Existence in Nature

Electric charge is present in all matter:

• On Earth: It causes frictional electricity (e.g. rubbing a balloon on hair), and enables electrical circuits.

• In the Atmosphere: Charge separation in clouds leads to lightning and thunderstorms.

• In Space: Charged particles (plasma) stream from the sun as solar wind; stars, including the sun, contain ionized gases.

• In Atoms: Charge is confined to the particles—protons (+), electrons (–), and neutrons (0).

---

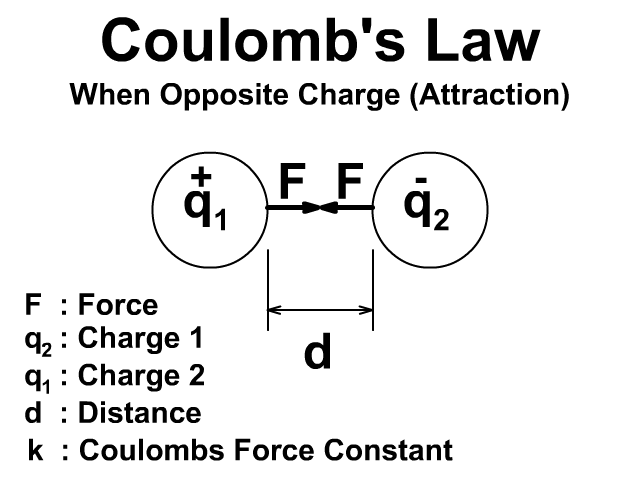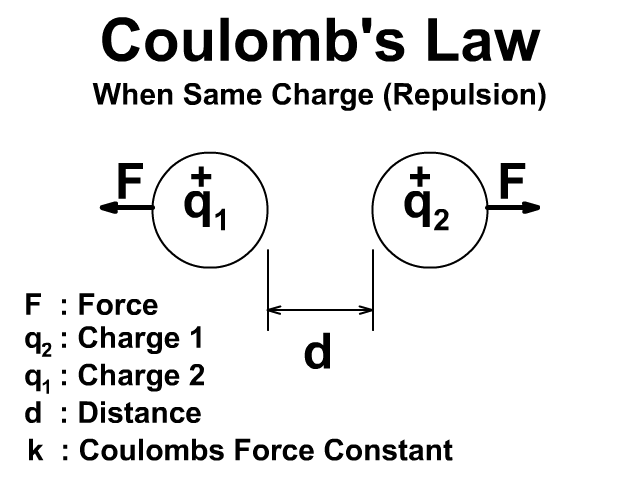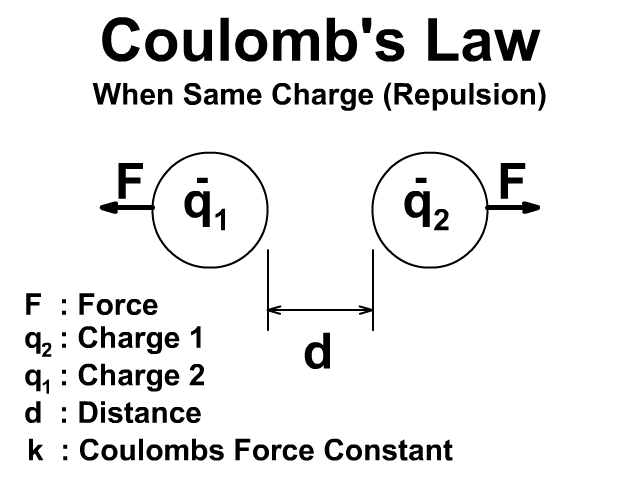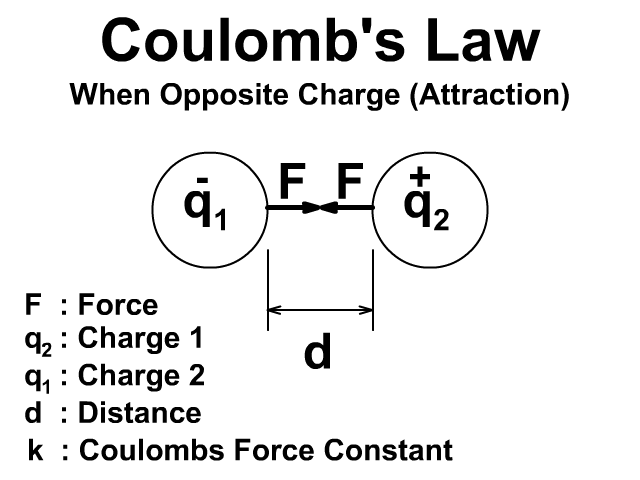
🔹 7. Coulomb’s Law (Force Between Charges)

Coulomb’s law describes the force between two point charges:

$$F = k \cdot \frac{|q_1 q_2|}{r^2}$$

Where:

• $F$ is the electrostatic force,

• $q_1$ and $q_2$ are the magnitudes of the charges,

• $r$ is the distance between them,

• $k = 8.99 \times 10^9 \, \text{Nm}^2/\text{C}^2$ (Coulomb constant).

👉 Force is attractive if charges are opposite, repulsive if same.

The electrostatic force (F) between two charges becomes weaker as the distance between them increases. More exactly, the force is inversely proportional to the square of the distance between the charges.

That means:

$$F \propto \frac{1}{r^2}$$

👉 If you double the distance, the force becomes 1/4 as strong.
👉 If you triple the distance, the force becomes 1/9 as strong.

So, as distance increases, the force drops off quickly — not just linearly, but by the square of that distance.

---

⚡ Coulomb’s Law – Complete Explanation

Let’s consider two point charges:

• $q_1$ and $q_2$

• At rest in vacuum

• Separated by a distance $r$

• 
  
  
  

---

📌 Coulomb’s Law Statement

According to Coulomb:

$$\vec{F}_{21} = k \cdot \frac{q_1 q_2}{r^2} \hat{r}_{12}$$

Where:

• $\vec{F}_{21}$: Force on $q_2$ due to $q_1$

• $k$: Coulomb constant $= 9 \times 10^9 \, \text{Nm}^2/\text{C}^2$

• $\hat{r}_{12}$: Unit vector pointing from $q_1$ to $q_2$

• $r$: Distance between the two point charges

---

📘 Important Aspects of Coulomb's Law

---

✅ (i) Force Depends on Product of Charges and Square of Distance

$$F \propto \frac{q_1 q_2}{r^2}$$

• If either charge increases, force increases.

• If distance increases, force decreases rapidly.

---

✅ (ii) Direction of Force Lies Along Line Joining the Charges

• The force acts along the straight line connecting the two charges.

• If both charges have the same sign, force is repulsive.

• If they have opposite signs, force is attractive.

$$\vec{F}_{21} = -\vec{F}_{12}$$

Each charge experiences equal and opposite force due to Newton’s Third Law.

---

✅ (iii) Coulomb Constant & Permittivity

In SI Units:

$$k = \frac{1}{4\pi\epsilon_0}, \quad \text{where } \epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{Nm}^2$$

• $\epsilon_0$ is called the permittivity of free space (vacuum).

 

---

✅ (v) Coulomb’s Law in Medium

In a medium other than vacuum:

$$\vec{F}_{21} = \frac{1}{4\pi\epsilon} \cdot \frac{q_1 q_2}{r^2} \hat{r}_{12}$$

Where:

• $\epsilon$: Permittivity of the medium

• Since $\epsilon > \epsilon_0$, the force is less in medium than in vacuum

🧠 Relative Permittivity (Dielectric Constant):

$$\epsilon_r = \frac{\epsilon}{\epsilon_0}$$

• In vacuum: $\epsilon_r = 1$

• In other media: $\epsilon_r > 1$

---

✅ (vi) Applicable to Point Charges Only

Coulomb’s law is strictly valid only for point charges, i.e., charges whose size is negligible compared to the distance $r$ between them.

---

🔹 8. Detection & Measurement of Charge

Instruments:

• Electroscope: Detects presence and type of charge.

• Electrometer: Precisely measures quantity of electric charge.

• Ammeter (indirect): Measures current to calculate charge over time.

---

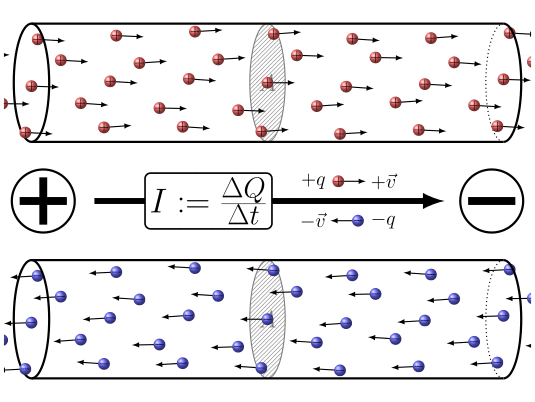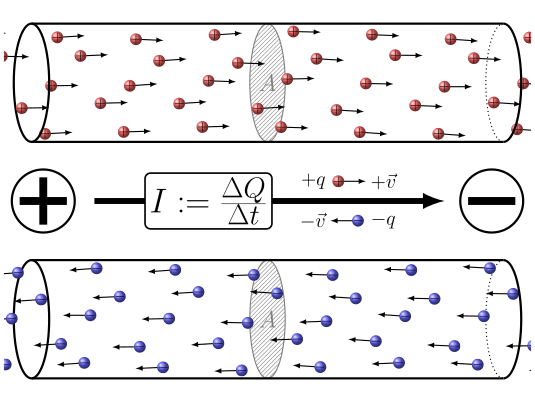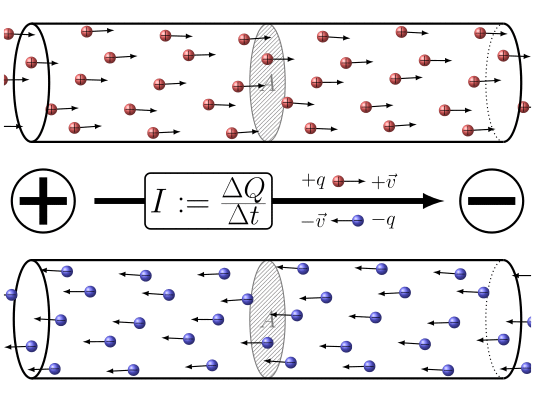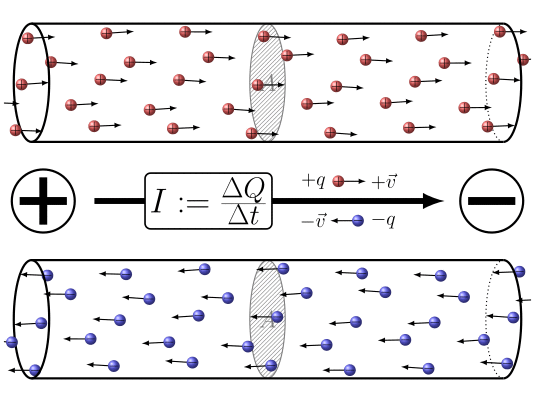
🔹 9. Electric Current – Movement of Charge

Electric current is the rate of flow of charge.

$$I = \frac{Q}{t}$$

Where:

• $I$ = current in amperes (A),

• $Q$ = total charge in coulombs (C),

• $t$ = time in seconds (s).

Electric current is the flow of electric charge in a conductor. By convention, we say current flows from the positive terminal to the negative terminal. But actually, the electrons, which carry the charge, move in the opposite direction—from negative to positive. So, electric current and electron flow are opposite to each other.

---

🔹 10. Electric Charge in the Universe (From Ground to Sky)

🌍 On Earth:

• Static electricity from contact/friction

• Lightning: massive electric discharge due to charge separation in clouds

• Electric power systems and devices

⚡ In the Atmosphere:

• Charged particles in clouds create electric fields

• Thunderstorms and auroras occur due to interaction of these charges with Earth’s magnetic field

🚀 In Space:

• Solar wind: a stream of charged particles (electrons, protons)

• Plasma: the fourth state of matter made of ionized gases

• Fusion in stars involves high-energy charged particle collisions

⚖️ Electrostatic Force vs Gravitational Force – With Similarities

Feature	Electrostatic Force	Gravitational Force
1. Nature	Can be attractive or repulsive	Always attractive
2. Obeys Inverse Square Law	✅ Yes: $F_e \propto \frac{1}{r^2}$	✅ Yes: $F_g \propto \frac{1}{r^2}$
3. Acts Over Distance	✅ Yes – long-range force	✅ Yes – long-range force
4. Medium Dependence	✅ Depends on the dielectric of the medium	❌ Independent of medium
5. Type of Interaction	Acts between electric charges	Acts between masses
6. Direction of Force	Repulsive (like charges) or Attractive (opposite charges)	Only attractive
7. Relative Strength	Very strong compared to gravity	Very weak, especially at atomic/molecular scale
8. Conservativeness	✅ Conservative – work done in closed path is zero	✅ Conservative – same property
9. Field Type	Electric Field (E-field)	Gravitational Field
10. Mathematical Form	$$F=k⋅q1.q2 / r^2	$$F=G⋅m1 . m2 / r^2
11. Force Carrier (Quantum)	Photon (in quantum theory)	Graviton (hypothetical)

---

✅ Similarities Between Electrostatic and Gravitational Forces

Similarity Aspect	Explanation
1. Inverse Square Law	Both decrease in strength with square of the distance: $\frac{1}{r^2}$
2. Conservative Forces	Work done in a closed path is zero; energy is conserved
3. Central Forces	Always act along the line joining two objects
4. Long-Range Forces	Can act over infinite distance without needing direct contact
5. Field Forces	Both create fields around them (electric field or gravitational field)
6. Superposition Principle	Both follow the superposition principle—forces from multiple sources add up

---

---

🔹 11. Applications of Electric Charge

Area	Use Case
Electronics	Batteries, transistors, logic circuits
Medicine	ECG, EEG, defibrillators
Communication	Radio, mobile phones, satellite links
Industry	Electroplating, electrostatic painting
Science	Particle accelerators, quantum mechanics

---

🔹 12. Charge in the Standard Model of Physics

In particle physics, charge is a quantum number. Quarks, for instance, carry fractional charges:

• Up quark: $+\frac{2}{3}e$

• Down quark: $-\frac{1}{3}e$

Electrons, protons, and other particles interact through the electromagnetic force based on their charge.

---

🔹 13. Band Theory & Energy Gap (Materials Science)

What is a Band Gap?

• Electrons in solids occupy energy levels forming bands.

• Valence band: filled with electrons.

• Conduction band: where free electrons move.

• The energy gap (or band gap) is the energy difference between them.

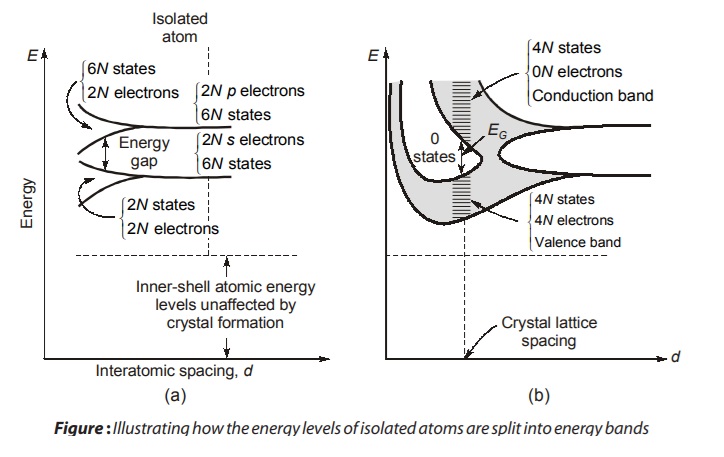
 Energy Bands in Solids – Conductors, Semiconductors & Insulators

---

🔹 Introduction to Energy Bands

In solid-state physics, energy bands describe the ranges of energy that an electron within a solid may have. These arise due to the overlap of atomic orbitals in a large collection of atoms (as in a crystal lattice). The three main classifications based on these bands are:

• Insulators

• Semiconductors

• Conductors (Metals)

These classifications are based on the band structure, especially:

• The valence band (filled or partially filled with electrons)

• The conduction band (where electrons can move freely)

• The forbidden gap (band gap) between them

---

🔹  Insulators

🔸 Definition:

An insulator is a material in which electrons cannot move freely due to a large energy gap between the valence and conduction bands.

🔍 Explanation:

• The forbidden energy gap is too large (~6 eV), so electrons in the valence band cannot jump to the conduction band under normal conditions.

• At room temperature, insulators do not conduct electricity.

• If extreme temperature or high voltage is applied, electrons may be excited across the gap, leading to dielectric breakdown.

🧪 Example: Diamond, Mica, Glass

---

🔹 Semiconductors

🔸 Definition:

A semiconductor is a material with a moderate energy gap (~1 eV), which allows some electrons to move into the conduction band under moderate thermal or optical excitation.

🔍 Explanation:

• At 0 K, semiconductors behave like insulators (no conduction).

• At room temperature, enough electrons gain thermal energy to jump the band gap.

• The conductivity increases with temperature or light — this is a key property used in electronics.

🔸 Types of Semiconductors:

• Intrinsic: Pure semiconductors like Si and Ge

• Extrinsic: Doped with impurities to form:

  • n-type (extra electrons)

  • p-type (holes)

🧪 Examples: Silicon (Si), Germanium (Ge), Gallium Arsenide (GaAs)

---

🔹  Conductors (Metals)

🔸 Definition:

A conductor (metal) is a material in which electrons can flow freely because the conduction and valence bands overlap — no band gap exists.

🔍 Explanation:

• Even without external energy, metals contain a large number of free electrons.

• These electrons can easily move under an electric field, making metals excellent conductors.

• Temperature has little effect on their conductivity compared to semiconductors.

🧪 Examples: Copper (Cu), Aluminum (Al), Silver (Ag)

---

🔸  Comparison between insulators , semiconductors & metal

Feature	Insulators	Semiconductors	Conductors (Metals)
Band Gap $E_g$	Large (~6 eV)	Small (~0.7–1.1 eV)	None or overlapping
Conduction Band	Empty	Partially filled at RT	Overlapping with VB
Valence Band	Full	Almost full	Partially filled
Free Electrons at RT	Almost none	Some	Many
Conductivity	Very low	Moderate (temperature-dependent)	Very high
Effect of Temperature	Little or none	Strong (↑ temp → ↑ σ)	Slightly decreases σ
Examples	Diamond, Mica	Si, Ge	Cu, Al, Ag

---

✅ Note:

Understanding energy bands is crucial in:

• Designing semiconductors and diodes

• Explaining electrical behavior of materials

• Creating advanced devices like transistors, LEDs, and solar cells

---

🔹 14. Effective Mass of Charge Carriers

In crystals, electrons respond differently than in a vacuum. Their effective mass is defined as:

$$m^* = \frac{\hbar^2}{\frac{d^2E}{dk^2}}$$

Where:

• $\hbar$ is reduced Planck's constant,

$E$ is energy,

• $k$ is the wave vector.

Smaller $m^*$ → higher mobility → better conductivity.

---

🔹 15. Doping and Carrier Mobility in Semiconductors

Understanding the role of doping and carrier mobility is central to semiconductor physics. These two concepts determine how well a semiconductor conducts electricity, which in turn underpins all modern electronics.

---

⚛️  Intrinsic vs Extrinsic Semiconductors

🔹 Intrinsic Semiconductors

• Definition: Pure semiconductors with no added impurities.

• Examples: Pure Silicon (Si) and Germanium (Ge).

• Charge Carriers: Electrons (negative) and holes (positive) are generated in equal numbers due to thermal excitation.

  $$n = p = n_i$$

  Where:

  • $n$: Electron concentration

  • $p$: Hole concentration

  • $n_i$: Intrinsic carrier concentration

• Properties:

  • Low electrical conductivity

  • High carrier mobility (since there are no impurity collisions)

  • Dominant scattering mechanism: lattice (phonon) vibrations

---

🔹 Extrinsic Semiconductors

• Definition: Semiconductors that have been intentionally doped with impurities to improve conductivity.

• Types:

  • n-type: Donor atoms add electrons

  • p-type: Acceptor atoms create holes

📌 n-type Doping (Donors)

• Adds: Extra electrons (majority carriers)

• Dopant Elements (Group V):

  • Phosphorus (P)

  • Arsenic (As)

  • Antimony (Sb) (not "An")

  • Bismuth (Bi) (less common)

• These atoms have 5 valence electrons — one more than Si or Ge — and donate the extra electron to the conduction band.

📌 p-type Doping (Acceptors)

• Creates: Holes (majority carriers)

• Dopant Elements (Group III):

  • Boron (B)

  • Gallium (Ga)

  • Indium (In)

• These have 3 valence electrons — one less than Si or Ge — creating a "hole" by accepting an electron.

---

⚙️ Carrier Mobility

Carrier mobility ($\mu$) is the measure of how quickly electrons or holes move through a semiconductor when subjected to an electric field.

• Units: cm²/(V·s)

• Types:

  • Electron mobility (μₙ) — typically higher

  • Hole mobility (μₚ) — typically lower

• Depends on:

  • Temperature (higher temp → more lattice scattering → lower mobility)

  • Doping level (more doping → more ionized impurity scattering → lower mobility)

  • Material type (e.g., GaAs has much higher mobility than Si)

---

🔄  Effect of Doping on Carrier Mobility

There is a trade-off between carrier concentration and mobility:

• At low doping, mobility is high, and conductivity increases with added carriers.

• At high doping, ionized impurity scattering increases, which reduces mobility, sometimes significantly.

📈 Mobility vs Doping

• Moderate doping increases conductivity efficiently.

• Excessive doping causes mobility to drop sharply due to carrier scattering, limiting further improvement in performance.

---

📐  Conductivity Equation of a semiconductor

The electrical conductivity of a semiconductor is given by:

$$\sigma = q \cdot n \cdot \mu$$

Where:

• $\sigma$: Conductivity (S/cm)

• $q$: Elementary charge (~1.6 × 10⁻¹⁹ C)

• $n$: Carrier concentration (cm⁻³)

• $\mu$: Carrier mobility (cm²/V·s)

🔹 In n-type: $n$ is the electron concentration and $\mu$ is $\mu_n$
🔹 In p-type: $p$ is the hole concentration and $\mu$ is $\mu_p$

---

📊  Difference between intrinsic & extrinsic semiconductors

Property	Intrinsic Semiconductor	Extrinsic Semiconductor
Carrier Concentration	Low ( $n = p = n_i$ )	High (due to doping)
Majority Carrier	Electrons = Holes	Electrons (n-type) or Holes (p-type)
Conductivity	Low	High
Carrier Mobility	High (low scattering)	Reduced (due to impurity scattering)
Dopants Used	None	Group V (n-type), Group III (p-type)

---

Advanced Concept – Mass Gap (Particle Physics)

In quantum field theory, a mass gap is the minimum energy difference between the vacuum and excited states. It’s crucial in Yang–Mills theory and explains why some particles have mass while photons don’t.

---

📌 Related Topics

• PCM in Digital Communication
• Electrostatics – Introduction
• Electromagnetics – Introduction